前回のブログで遡行学習の重要性について述べました。

遡行学習につい考えるために、新たに次の問題について考えてみましょう。

【問題】次の等式を[]内の文字について解きなさい。

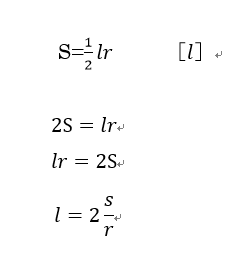
この数学の問題は式を変形する問題です。中学１年生で習います。しかし、アクロス個別指導学院の入塾時、体験授業の中で、中学三年生にこの問題を解いてもらうと、相当数の生徒が解けません。

この式の変形を順を追って解説すると次の様になります。

【最初の変形】　両辺に２を掛ける（分母を払う）

【二番目の変形】右辺と左辺を入れ替える

【三番目の変形】両辺を　ｒ　で割る

　この三つの変形を正しく行うことが出来れば正解にたどり着きます。
しかし、この三つの法則を連動させて、正解できる生徒は非常に少ないのです。

その原因は「途中式を書く事が身についていない」事にあります。

　男子では、「途中式を書くことがめんどくさい」と感じるために暗算とメモ書きを多用して計算間違いをしてしまうパターンが良く見受けられます。

　従ってこの問題を正しく解くための遡行学習の目的は「途中式を正しく書けるようにする事」になります。

小学生、中学生、高校生が算数、数学を解くには計算力は必要不可欠です。そして数学の学力はこの計算力支えられていることをまず認識する必要があります。
　数学を解くためには思考力は当然求められます。しかし、小学生、中学生の数学においてはテストでは思考力よりも計算力が重要です。都立高校の数学の入試問題を見ると、①番には９題あり７題は全くの計算問題です。これを全問正解すると３５点あります。

　以前、ゆとり世代の算数、数学の教科書に頻繁に【電卓マーク】が登場しました。筆算をしないで電卓で計算しなさいという意味です。
　人間に必要なのは思考力であり、計算は電卓、コンピューター任せればよい、という考え方です。
　しかし、現在の教科書ではこの考え方は排除されています。その理由は生徒の計算力があまりにも低下してそれにつれ学力も下がってしまったからです。

　実際に生徒を教えていて、小学生、中学生、高校生の数学の学力と計算力はほぼ比例しています。相関関係にあります。

　このような事実を踏まえて、アクロス個別指導学院では塾生全員が途中式が書けるよう指導を徹底しています。
これが数学が出来るようになる第一歩だからです。
 

　途中式に対する遡行学習を実施すると、塾生全員が「途中式を正しく書ける」様になります。これがベースになって数学力は向上していきます。
　計算力の重要性を再認識してください。

では再度、読者の皆さんに問題を提供します。

次の二問が正しく解けるでしょうか。

最初の問題は小学生の基礎知識で解けます。

　二番目は中学１年生の夏休み前後で習います。従って夏休みを過ぎた中学１年生以上は、この問題が解けなくてはいけません。

さてどうでしょうか。見事正解にたどりつけるでしょうか。挑戦してみてください。

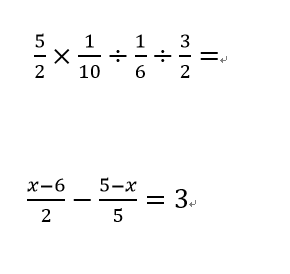
 　答え）最初の問題　１

　　　　二番目の問題　X＝１０

この問題が解けない事が判明したとすれば、遡行学習を実施して計算力、途中式を書く力を身に付けてください。

そうすれば数学の学力は一気に向上するはずです。

しかし逆の言い方をすればこの２つの問題がスラスラと途中式を書いて解けない場合は数学力は低いと見なければなりません。

　解けなければ即座に遡行学習です。

前回のブログでも触れたように、アクロス個別指導学院ではこのような事態が判明すれば即座に特訓授業を実施します。レギュラー授業以外に毎日塾に来て遡行学習をして頂きます。
　アクロス個別指導学院では、塾長の指示に従って授業に取り組むことを確認して頂ければ無料で遡行学習を実施しています。